

For n-D meshes dilation is at most 4n minus 1, marginally improving on the best sequential algorithm guaranteeing dilation at most 4n plus more » 1. For 3-D meshes, dilation, is at most eight, slightly worse than the best sequential algorithms guaranteeing dilation at most seven. For 2-D meshes dilation is at most two, which is optimal. Except for 3-D meshes, the dilation achieved here is no more than for the sequential algorithms. It is argued that hypercube embeddings should, if possible, be computed by parallel algorithms, underscoring the significance of the algorithms presented, since existing algorithms appear to be inherently sequential.
Parallel algorithms suitable for hypercube execution are given to embed any mesh in its optimal hypercube, thereby minimizing expansion.

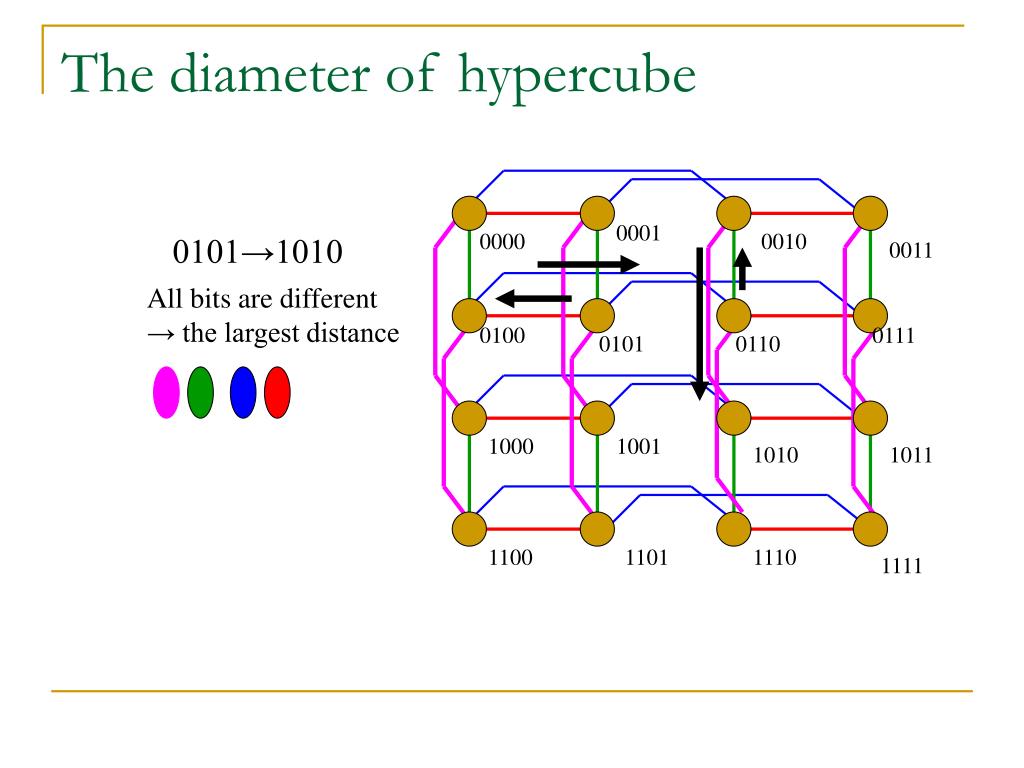
The embedding should keep certain simulation costs small, the most significant being dilation and expansion. This requires the communication graph of the preferred network be mapped, or embedded into that of the available one. The natural or preferred interconnection network implied by the communication needs of the parallel algorithm must be simulated by some actually available network whose interconnections are different from those of the preferred one. An n-cube can be constructed from two subcubes each having an (n- 1) degree by connecting nodes of similar addresses in both subcubes.The mapping problem arises whenever a parallel algorithm is implemented on an array of processors. One of the desirable features of hypercube networks is the recursive nature of their constructions. This is because the maximum number of links a message has to traverse to reach its destination in an n-cube containing N - 2n nodes is log2 N = n links. The hypercube is referred to as a logarithmic architecture. The upper limit on the number of disjoint paths in an n-cube is n. The degree of a node is defined as the number of links incident on the node. Once the message traverses the three dimensions in any order it will reach its destination. The order in which the message traverses the three dimensions is not important. That will mean that the message will be sent only along dimensions 2, 3, and 4 (counting from right to left) to arrive at the destination. If the XOR-ing operation results in a 1 in a given bit position, then the message has to be sent along with the link that spans the corresponding dimension.įor example, if a message is sent from source (S) node 0101 to destination (D) node 1011, then the XOR operation results in 1110. The route of a message originating at node i and destined for node j can be found by XOR-ing the binary address representation of i and j. This property allows for a simple message routing mechanism. In an n-cube, each processor has communication links to n other processors. Edges of the graph represent the point-to-point communication links between processors.Įach processor in a 4-cube is connected to four other processors. In a cube-based multiprocessor system, processing elements are positioned at the vertices of the graph. An n-cube (hypercube of order n) is defined as an undirected graph having 2n vertices labeled 0 to 2n - 1 such that there is an edge between a given pair of vertices if and only if the binary representation of their addresses differs by one and only one bit. Cube-connected networks are patterned after the n-cube structure.


 0 kommentar(er)
0 kommentar(er)
